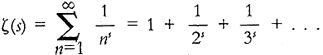
Let’s set the existence-of-God issue aside for a later volume, and just stipulate that in some way, self-replicating organisms came into existence on this planet and immediately began trying to get rid of each other, either by spamming their environments with rough copies of themselves, or by more direct means which hardly need to be belabored. Most of them failed, and their genetic legacy was erased from the universe forever, but a few found some way to survive and to propagate. After about three billion years of this sometimes zany, frequently tedious fugue of carnality and carnage, Godfrey Waterhouse IV was born, in Murdo, South Dakota, to Blanche, the wife of a Congregational preacher named Bunyan Waterhouse. Like every other creature on the face of the earth, Godfrey was, by birthright, a stupendous badass, albeit in the somewhat narrow technical sense that he could trace his ancestry back up a long line of slightly less highly evolved stupendous badasses to that first self-replicating gizmo—which, given the number and variety of its descendants, might justifiably be described as the most stupendous badass of all time. Everyone and everything that wasn’t a stupendous badass was dead.
As nightmarishly lethal, memetically programmed death-machines went, these were the nicest you could ever hope to meet. In the tradition of his namesake (the Puritan writer John Bunyan, who spent much of his life in jail, or trying to avoid it) the Rev. Waterhouse did not preach in any one place for long. The church moved him from one small town in the Dakotas to another every year or two. It is possible that Godfrey found the lifestyle more than a little alienating, for, sometime during the course of his studies at Fargo Congregational College, he bolted from the fold and, to the enduring agony of his parents, fell into worldly pursuits, and ended up, somehow, getting a Ph.D. in Classics from a small private university in Ohio. Academics being no less nomadic than Congregational preachers, he took work where he could find it. He became a Professor of Greek and Latin at Bolger Christian College (enrollment 322) in West Point, Virginia, where the Mattaponi and Pamunkey Rivers came together to form the estuarial James, and the loathsome fumes of the big paper mill permeated every drawer, every closet, even the interior pages of books. Godfrey’s young bride, née Alice Pritchard, who had grown up following her itinerant-preacher father across the vastnesses of eastern Montana—where air smelt of snow and sage—threw up for three months. Six months later she gave birth to Lawrence Pritchard Waterhouse.
The boy had a peculiar relationship with sound. When a fire engine passed, he was not troubled by the siren’s howl or the bell’s clang. But when a hornet got into the house and swung across the ceiling in a broad Lissajous, droning almost inaudibly, he cried in pain at the noise. And if he saw or smelled something that scared him, he would clap his hands over his ears.
One noise that troubled him not at all was the pipe organ in the chapel at Bolger Christian College. The chapel itself was nothing worth mentioning, but the organ had been endowed by the paper mill family and would have sufficed for a church four times the size. It nicely complemented the organist, a retired high school math teacher who felt that certain attributes of the Lord (violence and capriciousness in the Old Testament, majesty and triumph in the New) could be directly conveyed into the souls of the enpewed sinners through a kind of frontal sonic impregnation. That he ran the risk of blowing out the stained-glass windows was of no consequence since no one liked them anyway, and the paper mill fumes were gnawing at the interstitial lead. But after one little old lady too many staggered down the aisle after a service, reeling from tinnitus, and made a barbed comment to the minister about the exceedingly dramatic music, the organist was replaced.
Nevertheless, he continued to give lessons on the instrument. Students were not allowed to touch the organ until they were proficient at the piano, and when this was explained to Lawrence Pritchard Waterhouse, he taught himself, in three weeks, how to play a Bach fugue, and signed up for organ lessons. Since he was only five years old at the time, he was unable to reach both the manuals and the pedals, and had to play standing—or rather strolling, from pedal to pedal.
When Lawrence was twelve, the organ broke down. That paper mill family had not left any endowment for maintenance, so the math teacher decided to have a crack at it. He was in poor health and required a nimble assistant: Lawrence, who helped him open up the hood of the thing. For the first time in all those years, the boy saw what had been happening when he had been pressing those keys.
For each stop—each timbre, or type of sound, that the organ could make (viz. blockflöte, trumpet, piccolo)—there was a separate row of pipes, arranged in a line from long to short. Long pipes made low notes, short high. The tops of the pipes defined a graph: not a straight line but an upward-tending curve. The organist/math teacher sat down with a few loose pipes, a pencil, and paper, and helped Lawrence figure out why. When Lawrence understood, it was as if the math teacher had suddenly played the good part of Bach’s Fantasia and Fugue in G Minor on a pipe organ the size of the Spiral Nebula in Andromeda—the part where Uncle Johann dissects the architecture of the Universe in one merciless descending ever-mutating chord, as if his foot is thrusting through skidding layers of garbage until it finally strikes bedrock. In particular, the final steps of the organist’s explanation were like a falcon’s dive through layer after layer of pretense and illusion, thrilling or sickening or confusing depending on what you were. The heavens were riven open. Lawrence glimpsed choirs of angels ranking off into geometrical infinity.
The pipes sprouted in parallel ranks from a broad flat box of compressed air. All of the pipes for a given note—but belonging to different stops—lined up with each other along one axis. All of the pipes for a given stop—but tuned at different pitches—lined up with each other along the other, perpendicular axis. Down there in the flat box of air, then, was a mechanism that got air to the right pipes at the right times. When a key or pedal was depressed, all of the pipes capable of sounding the corresponding note would speak, as long as their stops were pulled out.
Mechanically, all of this was handled in a fashion that was perfectly clear, simple, and logical. Lawrence had supposed that the machine must be at least as complicated as the most intricate fugue that could be played on it. Now he had learned that a machine, simple in its design, could produce results of infinite complexity.
Stops were rarely used alone. They tended to be piled on top of each other in combinations that were designed to take advantage of the available harmonics (more tasty mathematics here!). Certain combinations in particular were used over and over again. Lots of blockflötes, in varying lengths, for the quiet Offertory, for example. The organ included an ingenious mechanism called the preset, which enabled the organist to select a particular combination of stops—stops he himself had chosen—instantly. He would punch a button and several stops would bolt out from the console, driven by pneumatic pressure, and in that instant the organ would become a different instrument with entirely new timbres.
The next summer both Lawrence and Alice, his mother, were colonized by a distant cousin—a stupendous badass of a virus. Lawrence escaped from it with an almost imperceptible tendency to drag one of his feet. Alice wound up in an iron lung. Later, unable to cough effectively, she got pneumonia and died.
Lawrence’s father, Godfrey, freely confessed that he was not equal to the burdens now laid on his shoulders. He resigned from his position at the small college in Virginia and moved, with his son, to a small house in Moorhead, Minnesota, next door to where Bunyan and Blanche had settled. Later he got a job teaching at a nearby normal school.
At this point, all of the responsible adults in Lawrence’s life seemed to arrive at a tacit agreement that the best way to raise him—certainly the easiest—was to leave him alone. On the rare occasions when Lawrence requested adult intervention in his life, he was usually asking questions that no one could answer. At the age of sixteen, having found nothing in the local school system to challenge him, Lawrence Pritchard Waterhouse went off to college. He matriculated at Iowa State College, which among other things was the site of a Naval ROTC installation in which he was forcibly enrolled.
The Iowa State Naval ROTC had a band, and was delighted to hear that Lawrence had an interest in music. Since it was hard to drill on the deck of a dreadnought while playing a pipe organ, they issued him a glockenspiel and a couple of little dingers.
When not marching back and forth on the flood plain of the Skunk River making loud dinging noises, Lawrence was majoring in mechanical engineering. He ended up doing poorly in this area because he had fallen in with a Bulgarian professor named John Vincent Atanasoff and his graduate student, Clifford Berry, who were building a machine that was intended to automate the solution of some especially tedious differential equations.
The basic problem for Lawrence was that he was lazy. He had figured out that everything was much simpler if, like Superman with his X-ray vision, you just stared through the cosmetic distractions and saw the underlying mathematical skeleton. Once you found the math in a thing, you knew everything about it, and you could manipulate it to your heart’s content with nothing more than a pencil and a napkin. He saw it in the curve of the silver bars on his glockenspiel, saw it in the catenary arch of a bridge and in the capacitor-studded drum of Atanasoff and Berry’s computing machine. Actually pounding on the glockenspiel, riveting the bridge together, or trying to figure out why the computing machine wasn’t working were not as interesting to him.
Consequently he got poor grades. From time to time, though, he would perform some stunt on the blackboard that would leave his professor weak in the knees and the other students baffled and hostile. Word got around.
At the same time, his grandmother Blanche was invoking her extensive Congregational connections, working the angles on Lawrence’s behalf, totally unbeknownst to him. Her efforts culminated in triumph when Lawrence was awarded an obscure scholarship, endowed by a St. Paul oat-processing heir, whose purpose was to send Midwestern Congregationalists to the Ivy League for one year, which (evidently) was deemed a long enough period of time to raise their IQs by a few crucial points but not long enough to debauch them. So Lawrence got to be a sophomore in Princeton.
Now Princeton was an august school and going there was a great honor, but no one got around to mentioning either of these facts to Lawrence, who had no way of knowing. This had bad and good consequences. He accepted the scholarship with a faintness of gratitude that infuriated the oat lord. On the other hand, he adjusted to Princeton easily because it was just another place . It reminded him of the nicer bits of Virginia, and there were some nice pipe organs in town, though he was not all that happy with his engineering homework of bridge-designing and sprocket-cutting problems. As always, these eventually came down to math, most of which he could handle easily. From time to time he would get stuck, though, which led him to the Fine Hall: the headquarters of the Math Department.
There was a motley assortment of fellows wandering around in Fine Hall, many sporting British or European accents. Administratively speaking, many of these fellows were not members of the Math Department at all, but a separate thing called IAS, which stood for Institute for Advanced something-or-other. But they were all in the same building and they all knew a thing or two about math, so the distinction didn’t exist for Lawrence.
Quite a few of these men would pretend shyness when Lawrence sought their advice, but others were at least willing to hear him out. For example: he had come up with a way to solve a difficult sprocket tooth shape problem that, as normally solved by engineers, would require any number of perfectly reasonable but aesthetically displeasing approximations. Lawrence’s solution would provide exact results. The only drawback was that it would require a quintillion slide-rule operators a quintillion years to solve. Lawrence was working on a radically different approach that, if it worked, would bring those figures down to a trillion and a trillion respectively. Unfortunately, Lawrence was unable to interest anyone at Fine Hall in anything as prosaic as gears, until all of a sudden he made friends with an energetic British fellow, whose name he promptly forgot, but who had been doing a lot of literal sprocket-making himself lately. This fellow was trying to build, of all things, a mechanical calculating machine—specifically a machine to calculate certain values of the Riemann Zeta Function
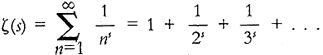
where s is a complex number.
Lawrence found this zeta function to be no more and no less interesting than any other math problem until his new friend assured him that it was frightfully important, and that some of the best mathematicians in the world had been gnawing on it for decades. The two of them ended up staying awake until three in the morning working out the solution to Lawrence’s sprocket problem. Lawrence presented the results proudly to his engineering professor, who snidely rejected it, on grounds of practicality, and gave him a poor grade for his troubles.
Lawrence finally remembered, after several more contacts, that the name of the friendly Brit was Al something-or-other. Because Al was a passionate cyclist, he and Al went on quite a few bicycle rides through the countryside of the Garden State. As they rode around New Jersey, they talked about math, and particularly about machines for taking the dull part of math off their hands.
But Al had been thinking about this subject for longer than Lawrence, and had figured out that computing machines were much more than just labor-saving devices. He’d been working on a radically different sort of computing mechanism that would work out any arithmetic problem whatsoever, as long as you knew how to write the problem down. From a pure logic standpoint, he had already figured out everything there was to know about this (as yet hypothetical) machine, though he had yet to build one. Lawrence gathered that actually building machinery was looked on as undignified at Cambridge (England, that is, where this Al character was based) or for that matter at Fine Hall. Al was thrilled to have found, in Lawrence, someone who did not share this view.
Al delicately asked him, one day, if Lawrence would terribly mind calling him by his full and proper name, which was Alan and not Al. Lawrence apologized and said he would try very hard to keep it in mind.
One day a couple of weeks later, as the two of them sat by a running stream in the woods above the Delaware Water Gap, Alan made some kind of an outlandish proposal to Lawrence involving penises. It required a great deal of methodical explanation, which Alan delivered with lots of blushing and stuttering. He was ever so polite, and several times emphasized that he was acutely aware that not everyone in the world was interested in this sort of thing.
Lawrence decided that he was probably one of those people.
Alan seemed vastly impressed that Lawrence had paused to think about it at all and apologized for putting him out. They went directly back to a discussion of computing machines, and their friendship continued unchanged. But on their next bicycle ride—an overnight camping trip to the Pine Barrens—they were joined by a new fellow, a German named Rudy von something-or-other.
Alan and Rudy’s relationship seemed closer, or at least more multilayered, than Alan and Lawrence’s. Lawrence concluded that Alan’s penis scheme must have finally found a taker.
It got Lawrence to thinking. From an evolution standpoint, what was the point of having people around who were not inclined to have offspring? There must be some good, and fairly subtle, reason for it.
The only thing he could work out was that it was groups of people—societies—rather than individual creatures, who were now trying to out-reproduce and/or kill each other, and that, in a society, there was plenty of room for someone who didn’t have kids as long as he was up to something useful.
Alan and Rudy and Lawrence rode south, anyway, looking for the Pine Barrens. After a while the towns became very far apart, and the horse farms gave way to a low stubble of feeble, spiny trees that appeared to extend all the way to Florida—blocking their view, but not the head wind. "Where are the Pine Barrens I wonder?" Lawrence asked a couple of times. He even stopped at a gas station to ask someone that question. His companions began to make fun of him.
"Vere are ze Pine Barrens?" Rudy inquired, looking about quizzically.
"I should look for something rather barren-looking, with numerous pine trees," Alan mused.
There was no other traffic and so they had spread out across the road to pedal three abreast, with Alan in the middle.
"A forest, as Kafka would imagine it," Rudy muttered.
By this point Lawrence had figured out that they were, in fact, in the Pine Barrens. But he didn’t know who Kafka was. "A mathematician?" he guessed.
"Zat is a scary sing to sink of," Rudy said.
"He is a writer," Alan said. "Lawrence, please don’t be offended that I ask you this, but: do you recognize any other people’s names at all? Other than family and close friends, I mean."
Lawrence must have looked baffled. "I’m trying to figure out whether it all comes from in here," Alan said, reaching out to rap his knuckles on the side of Lawrence’s head, "or do you sometimes take in new ideas from other human beings?"
"When I was a little boy, I saw angels in a church in Virginia," Lawrence said, "but I think that they came from inside my head."
"Very well," Alan said.
But later Alan had another go at it. They had reached the fire lookout tower and it had been a thunderous disappointment: just an alienated staircase leading nowhere, and a small cleared area below that was glittery with shards of liquor bottles. They pitched their tent by the side of a pond that turned out to be full of rust-colored algae that stuck to the hairs on their bodies. Then there was nothing left to do but drink schnapps and talk about math.
Alan said, "Look, it’s like this: Bertrand Russell and another chap named Whitehead wrote Principia Mathematica."
"Now I know you’re pulling my leg," Waterhouse said. "Even I know that Sir Isaac Newton wrote that."
"Newton wrote a different book, also called Principia Mathematica , which isn’t really about mathematics at all; it’s about what we would today call physics."
"Then why did he call it Principia Mathematica?"
"Because the distinction between mathematics and physics wasn’t especially clear in Newton’s day—"
"Or maybe even in zis day," Rudy said.
"—which is directly relevant to what I’m talking about," Alan continued. "I am talking about Russell’s P.M., in which he and Whitehead started absolutely from scratch, I mean from nothing, and built it all up—all mathematics—from a small number of first principles. And why I am telling you this, Lawrence, is that—Lawrence! Pay attention!"
"Hmmm?"
"Rudy—take this stick, here—that’s right—and keep a close eye on Lawrence, and when he gets that foggy look on his face, poke him with it!"
"Zis is not an English school, you can’t do zese kind of sing."
"I’m listening," Lawrence said.
"What came out of P.M., which was terrifically radical, was the ability to say that all of math, really, can be expressed as a certain ordering of symbols."
"Leibniz said it a long time before zen!" protested Rudy.
"Er, Leibniz invented the notation we use for calculus, but—"
"I’m not talking about zat!"
"And he invented matrices, but—"
"I’m not talking about zat eezer!"
"And he did some work with binary arithmetic, but—"
"Zat is completely different!"
"Well, what the hell are you talking about, then, Rudy?"
"Leibniz invented ze basic alphabet—wrote down a set of symbols, for expressing statements about logic."
"Well, I wasn’t aware that Herr Leibniz counted formal logic among his interests, but—"
"Of course! He wanted to do what Russell and Whitehead did, except not just with mathematics, but with everything in ze whole world!"
"Well, from the fact that you are the only man on the planet, Rudy, who seems to know about this undertaking of Leibniz’s, can we assume that he failed?"
"You can assume anything that pleases your fancy, Alan," Rudy responded, "but I am a mathematician and I do not assume anything."
Alan sighed woundedly, and gave Rudy a Significant Look which Waterhouse assumed meant that there would be trouble later. "If I may just make some headway, here," he said, "all I’m really trying to get you to agree on, is that mathematics can be expressed as a series of symbols," (he snatched the Lawrence-poking stick and began drawing things like + = 3) [square root -1] [pi] in the dirt) "and frankly I could not care less whether they happen to be Leibniz’s symbols, or Russell’s, or the hexagrams of the I Ching...."
"Leibniz was fascinated by the I Ching!" Rudy began.
"Shut up about Leibniz for a moment, Rudy, because look here: You—Rudy—and I are on a train, as it were, sitting in the dining car, having a nice conversation, and that train is being pulled along at a terrific clip by certain locomotives named The Bertrand Russell and Riemann and Euler and others. And our friend Lawrence is running alongside the train, trying to keep up with us—it’s not that we’re smarter than he is, necessarily, but that he’s a farmer who didn’t get a ticket. And I, Rudy, am simply reaching out through the open window here, trying to pull him onto the fucking train with us so that the three of us can have a nice little chat about mathematics without having to listen to him panting and gasping for breath the whole way."
"All right, Alan."
"Won’t take a minute if you will just stop interrupting."
"But there is a locomotive too named Leibniz."
"Is it that you don’t think I give enough credit to Germans? Because I am about to mention a fellow with an umlaut."
"Oh, would it be Herr Türing?" Rudy said slyly.
"Herr Türing comes later. I was actually thinking of Gödel."
"But he’s not German! He’s Austrian!"
"I’m afraid that it’s all the same now, isn’t it?"
"Ze Anschluss wasn’t my idea, you don’t have to look at me that way, I think Hitler is appalling."
"I’ve heard of Gödel," Waterhouse put in helpfully. "But could we back up just a sec?"
"Of course Lawrence."
"Why bother? Why did Russell do it? Was there something wrong with math? I mean, two plus two equals four, right?"
Alan picked up two bottlecaps and set them down on the ground. "Two. One-two. Plus—" He set down two more. "Another two. One-two. Equals four. One-two-three-four."
"What’s so bad about that?" Lawrence said.
"But Lawrence—when you really do math, in an abstract way, you’re not counting bottlecaps, are you?"
"I’m not counting anything."
Rudy broke the following news: "Zat is a very modern position for you to take."
"It is?"
Alan said, "There was this implicit belief, for a long time, that math was a sort of physics of bottlecaps. That any mathematical operation you could do on paper, no matter how complicated, could be reduced—in theory, anyway—to messing about with actual physical counters, such as bottlecaps, in the real world."
"But you can’t have two point one bottlecaps."
"All right, all right, say we use bottlecaps for integers, and for real numbers like two point one, we use physical measurements, like the length of this stick." Alan tossed the stick down next to the bottlecaps.
"Well what about pi, then? You can’t have a stick that’s exactly pi inches long."
"Pi is from geometry—ze same story," Rudy put in.
"Yes, it was believed that Euclid’s geometry was really a kind of physics, that his lines and so on represented properties of the physical world. But—you know Einstein?"
"I’m not very good with names."
"That white-haired chap with the big mustache?"
"Oh, yeah," Lawrence said dimly, "I tried to ask him my sprocket question. He claimed he was late for an appointment or something."
"That fellow has come up with a general relativity theory, which is sort of a practical application, not of Euclid’s, but of Riemann’s geometry—"
"The same Riemann of your zeta function?"
"Same Riemann, different subject. Now let’s not get sidetracked here Lawrence—"
"Riemann showed you could have many many different geometries that were not the geometry of Euclid but that still made sense internally," Rudy explained.
"All right, so back to P.M. then," Lawrence said.
"Yes! Russell and Whitehead. It’s like this: when mathematicians began fooling around with things like the square root of negative one, and quaternions, then they were no longer dealing with things that you could translate into sticks and bottlecaps. And yet they were still getting sound results."
"Or at least internally consistent results," Rudy said.
"Okay. Meaning that math was more than a physics of bottlecaps."
"It appeared that way, Lawrence, but this raised the question of was mathematics really true or was it just a game played with symbols? In other words—are we discovering Truth, or just wanking?"
"It has to be true because if you do physics with it, it all works out! I’ve heard of that general relativity thing, and I know they did experiments and figured out it was true."
"Ze great majority of mathematics does not lend itself to experimental testing," Rudy said.
"The whole idea of this project is to sever the ties to physics," Alan said.
"And yet not to be vanking ourselves."
"That’s what P.M. was trying to do?"
"Russell and Whitehead broke all mathematical concepts down into brutally simple things like sets. From there they got to integers, and so on."
"But how can you break something like pi down into a set?"
"You can’t," Alan said, "but you can express it as a long string of digits. Three point one four one five nine, and so on."
"And digits are integers," Rudy said.
"But no fair! Pi itself is not an integer!"
"But you can calculate the digits of pi, one at a time, by using certain formulas. And you can write down the formulas like so!" Alan scratched this in the dirt:
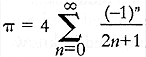
"I have used the Leibniz series in order to placate our friend. See, Lawrence? It is a string of symbols."
"Okay. I see the string of symbols," Lawrence said reluctantly.
"Can we move on? Gödel said, just a few years ago, ‘Say! If you buy into this business about mathematics being just strings of symbols, guess what?’ And he pointed out that any string of symbols—such as this very formula, here—can be translated into integers."
"How?"
"Nothing fancy, Lawrence—it’s just simple encryption. Arbitrary. The number ‘538’ might be written down instead of this great ugly [sigma], and so on.
"Seems pretty close to wanking, now."
"No, no. Because then Gödel sprang the trap! Formulas can act on numbers, right?"
"Sure. Like 2x."
"Yes. You can substitute any number for x and the formula 2x will double it. But if another mathematical formula, such as this one right here, for calculating pi, can be encoded as a number, then you can have another formula act on it. Formulas acting on formulas!"
"Is that all?"
"No. Then he showed, really through a very simple argument, that if formulas really can refer to themselves, it’s possible to write one down saying ‘this statement cannot be proved.’ Which was tremendously startling to Hilbert and everyone else, who expected the opposite result."
"Have you mentioned this Hilbert guy before?"
"No, he is new to this discussion, Lawrence."
"Who is he?"
"A man who asks difficult questions. He asked a whole list of them once. Gödel answered one of them."
"And Türing answered another," Rudy said.
"Who’s that?"
"It’s me," Alan said. "But Rudy’s joking. ‘Turing’ doesn’t really have an umlaut in it."
"He’s going to have an umlaut in him later tonight," Rudy said, looking at Alan in a way that, in retrospect, years later, Lawrence would understand to have been smoldering.
"Well, don’t keep me in suspense. Which one of his questions did you answer?"
"The Entscheidungsproblem," Rudy said.
"Meaning?"
Alan explained, "Hilbert wanted to know whether any given statement could, in principle, be found true or false."
"But after Gödel got finished, it changed," Rudy pointed out.
"That’s true—after Gödel it became ‘Can we determine whether any given statement is provable or non-provable?’ In other words, is there some sort of mechanical process we could use to separate the provable statements from the nonprovable ones?"
"‘Mechanical process’ is supposed to be a metaphor, Alan. . ."
"Oh, stop it, Rudy! Lawrence and I are quite comfortable with machinery."
"I get it," Lawrence said.
"What do you mean, you get it?" Alan said.
"Your machine—not the zeta-function calculator, but the other one. The one we’ve been talking about building—"
"It is called Universal Turing Machine," Rudy said.
"The whole point of that gizmo is to separate provable from nonprovable statements, isn’t it?"
"That’s why I came up with the basic idea for it," Alan said. "So Hilbert’s question has been answered. Now I just want to actually build one so that I can beat Rudy at chess."
"You haven’t told poor Lawrence the answer yet!" Rudy protested.
"Lawrence can figure it out," Alan said. "It’ll give him something to do."
Soon it became clear that Alan really meant: It’ll give him something to do while we’re fucking. Lawrence shoved a notebook into the waistband of his trousers and rode his bicycle a few hundred yards to the fire tower, then climbed up the stairs to the platform at the top and sat down, back to the setting sun, notebook propped up on his knees to catch the light.
He could not collect his thoughts, and then he was distracted by a false sunrise that lit up the clouds off to the northeast. He thought at first that some low clouds were bouncing fragments of the sunset back to him, but it was too concentrated and flickering for that. Then he thought it was lightning. But the color of the light was not blue enough. It fluctuated sharply, modulated by (one had to assume) great, startling events that were occulted by the horizon. As the sun went down on the opposite side of the world, the light on the New Jersey horizon focused to a steady, lambent core the color of a flashlight when you shine it through the palm of your hand under the bedsheets.
Lawrence climbed down the stairs and got on his bicycle and rode through the Pine Barrens. Before long he came to a road that led in the general direction of the light. Most of the time he could not see anything, not even the road, but after a couple of hours the glow bouncing off the low cloud layer lit up flat stones in the road, and turned the barrens’ wandering rivulets into glowing crevices.
The road began to tend in the wrong direction and so Lawrence cut directly into the woods, because he was very close now, and the light in the sky was strong enough that he could see it through the sparse carpet of scrubby pines—black sticks that appeared to have been burned, though they hadn’t. The ground had turned into sand, but it was damp and compacted, and his bicycle had fat tires that rode over it well. At one point he had to stop and throw the bike over a barbed-wire fence. Then he broke out of the sticks and onto a perfectly flat expanse of white sand, stitched down with tufts of beach grass, and just then he was dazzled by a low fence of quiet steady flames that ran across a part of the horizon about as wide as the harvest moon when it sinks into the sea. Its brightness made it difficult to see anything else—Lawrence kept riding into little ditches and creeks that meandered across the flats. He learned not to stare directly at the flames. Looking off to the sides was more interesting anyway: the table-land was marked at wide intervals by the largest buildings he had ever seen, cracker-box structures built by Pharaohs, and in the mile-wide plazas between them, gnomons of triangulated steel were planted in wide stances: the internal skeletons of pyramids. The largest of these pierced the center of a perfectly circular railway line a few hundred feet in diameter: two argent curves scored on the dull ground, interrupted in one place where the tower’s shadow, a stopped sundial, told the time. He rode by a building smaller than the others, with oval tanks standing next to it. Steam murmured from valves on the tops of the tanks, but instead of rising into the air it dribbled down the sides and struck the ground and spread out, coating the sea-grass with jackets of silver.
A thousand sailors in white were standing in a ring around the long flame. One of them held up his hand and waved Lawrence down. Lawrence came to a stop next to the sailor and planted one foot on the sand to steady himself. He and the sailor stared at each other for a moment and then Lawrence, who could not think of anything else, said, "I am in the Navy also." Then the sailor seemed to make up his mind about something. He saluted Lawrence through, and pointed him towards a small building off to the side of the fire.
The building looked only like a wall glowing in the firelight, but sometimes a barrage of magnesium blue light made its windowframes jump out of the darkness, a rectangular lightning-bolt that echoed many times across the night. Lawrence started pedaling again and rode past that building: a spiraling flock of alert fedoras, prodding at slim terse notebooks with stately Ticonderogas, crab-walking photogs turning their huge chrome daisies, crisp rows of people sleeping with blankets over their faces, a sweating man with Brilliantined hair chalking umlauted names on a blackboard. Finally coming around this building he smelled hot fuel oil, felt the heat of the flames on his face and saw beach-glass curled toward it and desiccated.
He stared down upon the world’s globe, not the globe fleshed with continents and oceans but only its skeleton: a burst of meridians, curving backwards to cage an inner dome of orange flame. Against the light of the burning oil those longitudes were thin and crisp as a draftsman’s ink-strokes. But coming closer he saw them resolve into clever works of rings and struts, hollow as a bird’s bones. As they spread away from the pole they sooner or later began to wander, or split into bent parts, or just broke off and hung in the fire oscillating like dry stalks. The perfect geometry was also mottled, here and there, by webs of cable and harnesses of electrical wiring. Lawrence almost rode over a broken wine bottle and decided he should now walk, to spare his bicycle’s tires, so he laid the bike down, the front wheel covering an aluminum vase that appeared to have been spun on a lathe, with a few charred roses hanging out of it. Some sailors had joined their hands to form a sort of throne, and were bearing along a human-shaped piece of charcoal dressed in a coverall of immaculate asbestos. As they walked the toes of their shoes caught in vast, ramified snarls of ropes and piano-wires, cables and wires, creative furtive movements in the grass and the sand dozens of yards every direction. Lawrence began planting his feet very thoughtfully one in front of the other, trying to measure the greatness of what he had come and seen. A rocket-shaped pod stuck askew from the sand, supporting an umbrella of bent-back propellers. The duralumin struts and catwalks rambled on above him for miles. There was a suitcase spilled open, with a pair of women’s shoes displayed as if in the window of a downtown store, and a menu that had been charred to an oval glow, and then some tousled wall-slabs, like a whole room that had dropped out of the sky—these were decorated, one with a giant map of the world, great circles arcing away from Berlin to pounce on cities near and far, and another with a photograph of a famous, fat German in a uniform, grinning on a flowered platform, the giant horizon of a new Zeppelin behind him.
After a while he stopped seeing new things. Then he got on his bicycle and rode back through the Pine Barrens. He got lost in the dark and so didn’t find his way back to the fire tower until dawn. But he didn’t mind being lost because while he rode around in the dark he thought about the Turing machine. Finally he came back to the shore of the pond where they had camped. The dawn-light shining on the saucer of calm reddish water made it look like a pool of blood. Alan Mathison Turing and Rudolf von Hacklheber were lying together like spoons on the shore, still smudged a little bit from their swim yesterday. Lawrence started a little fire and made some tea and they woke up eventually.
"Did you solve the problem?" Alan asked him.
"Well you can turn that Universal Turing Machine of yours into any machine by changing the presets—"
"Presets?"
"Sorry, Alan, I think of your U.T.M. as being kind of like a pipe organ."
"Oh."
"Once you’ve done that, anyway, you can do any calculation you please, if the tape is long enough. But gosh, Alan, making a tape that’s long enough, and that you can write symbols on, and erase them, is going to be sort of tricky—Atanasoff’s capacitor drum would only work up to a certain size—you’d have to—"
"This is a digression," Alan said gently.
"Yeah, okay, well—if you had a machine like that, then any given preset could be represented by a number—a string of symbols. And the tape that you would feed into it to start the calculation would contain another string of symbols. So it’s Gödel’s proof all over again—if any possible combination of machine and data can be represented by a string of numbers, then you can just arrange all of the possible strings of numbers into a big table, and then it turns into a Cantor diagonal type of argument, and the answer is that there must be some numbers that cannot be computed."
"And ze Entscheidungsproblem?" Rudy reminded him.
"Proving or disproving a formula—once you’ve encrypted the formula into numbers, that is—is just a calculation on that number. So it means that the answer to the question is, no! Some formulas cannot be proved or disproved by any mechanical process! So I guess there’s some point in being human after all!"
Alan looked pleased until Lawrence said this last thing, and then his face collapsed. "Now there you go making unwarranted assumptions."
"Don’t listen to him, Lawrence!" Rudy said. "He’s going to tell you that our brains are Turing machines."
"Thank you, Rudy," Alan said patiently. "Lawrence, I submit that our brains are Turing machines."
"But you proved that there’s a whole lot of formulas that a Turing machine can’t process!"
"And you have proved it too, Lawrence."
"But don’t you think that we can do some things that a Turing machine couldn’t?"
"Gödel agrees with you, Lawrence," Rudy put in, "and so does Hardy."
"Give me one example," Alan said.
"Of a noncomputable function that a human can do, and a Turing machine can’t?"
"Yes. And don’t give me any sentimental nonsense about creativity. I believe that a Universal Turing Machine could show behaviors that we would construe as creative."
"Well, I don’t know then . . . I’ll try to keep my eye out for that kind of thing in the future.’’
But later, as they were tiding back towards Princeton, he said, "What about dreams?"
"Like those angels in Virginia?"
"I guess so."
"Just noise in the neurons, Lawrence."
"Also I dreamed last night that a zeppelin was burning."
Soon, Alan got his Ph.D. and went back to England. He wrote Lawrence a couple of letters. The last of these stated, simply, that he would not be able to write Lawrence any more letters "of substance" and that Lawrence should not take it personally. Lawrence perceived right away that Alan’s society had put him to work doing something useful—probably figuring out how to keep it from being eaten alive by certain of its neighbors. Lawrence wondered what use America would find for him.
He went back to Iowa State, considered changing his major to mathematics, but didn’t. It was the consensus of all whom he consulted that mathematics, like pipe-organ restoration, was a fine thing, but that one needed some way to put bread on the table. He remained in engineering and did more and more poorly at it until the middle of his senior year, when the university suggested that he enter a useful line of work, such as roofing. He walked straight out of college into the waiting arms of the Navy.
They gave him an intelligence test. The first question on the math part had to do with boats on a river: Port Smith is 100 miles upstream of Port Jones. The river flows at 5 miles per hour. The boat goes through water at 10 miles per hour. How long does it take to go from Port Smith to Port Jones? How long to come back?
Lawrence immediately saw that it was a trick question. You would have to be some kind of idiot to make the facile assumption that the current would add or subtract 5 miles per hour to or from the speed of the boat. Clearly, 5 miles per hour was nothing more than the average speed. The current would be faster in the middle of the river and slower at the banks. More complicated variations could be expected at bends in the river. Basically it was a question of hydrodynamics, which could be tackled using certain well-known systems of differential equations. Lawrence dove into the problem, rapidly (or so he thought) covering both sides of ten sheets of paper with calculations. Along the way, he realized that one of his assumptions, in combination with the simplified Navier Stokes equations, had led him into an exploration of a particularly interesting family of partial differential equations. Before he knew it, he had proved a new theorem. If that didn’t prove his intelligence, what would?
Then the time bell rang and the papers were collected. Lawrence managed to hang onto his scratch paper. He took it back to his dorm, typed it up, and mailed it to one of the more approachable math professors at Princeton, who promptly arranged for it to be published in a Parisian mathematics journal.
Lawrence received two free, freshly printed copies of the journal a few months later, in San Diego, California, during mail call on board a large ship called the U.S.S. Nevada. The ship had a band, and the Navy had given Lawrence the job of playing the glockenspiel in it, because their testing procedures had proven that he was not intelligent enough to do anything else.
The sack of mail carrying Lawrence’s contribution to the mathematical literature arrived just in the nick of time. Lawrence’s ship, and quite a few of her sisters, had until then been based in California. But at just this moment, all of them were transferred to some place called Pearl Harbor, Hawaii, in order to show the Nips who was boss.
Lawrence had never really known what he wanted to do with his life, but he quickly decided that being glockenspiel player on a battleship in Hawaii during peacetime was a long way from the worst life you could possibly have. The harshest part of the job was sometimes having to sit or march in very warm conditions, and enduring occasional fluffed notes by other band members. He had abundant free time, which he spent working on a series of new theorems in the field of information theory. The field had been invented and pretty much encompassed by his friend Alan, but there was much detail work to be done. He and Alan and Rudy had sketched out a general plan of what needed to be proved or disproved. Lawrence tore through the list. He wondered what Alan and Rudy were up to in Britain and Germany, but he couldn’t write to them and find out, so he kept his work to himself. When he wasn’t playing the glockenspiel or working out theorems, there were bars and dances to go to. Waterhouse did some penis work of his own, got the clap, had it cured *, bought condoms. All of the sailors did this. They were like three-year olds who shove pencils in their ears, discover that it hurts, and stop doing it. Lawrence’s first year went by almost instantly. Time just blazed by. Nowhere could be sunnier, more relaxing, than Hawaii.